Formal Language Theory

Formal Language Theory 形式语言理论

什么是形式语言？/ 语言的形式定义

形式语言（Formal Language）是用精确的数学/及其可处理的公式定义的语言。一般作为一个集合出现。

语言定义在某一个特定的字母表上，字母表可以为任意有限集合（一般由$\Sigma$表示）。例如集合${a, b, c…, z}$就表示所有小写字母构成的字母表。

而字符串就是字母表中元素构成的有穷序列。

所以直觉上，一个语言是字母表所能构成的所有串的集合的一个子集。

语言的表示方法

不像自然语言，一个形式语言作为一个集合，需要有某种明确的标准来定义一个字符串是否是他的元素。定义方法主要有如下几种。

• 枚举法
• 形式文法（Formal Grammars，也叫做Phrase Structure Grammars）
• 正则文法（Regular Grammars）
• 自动机（图灵机、有限状态自动机）（Automata）

Formal Grammars （形式文法）

在形式语言理论中，形式文法是形式语言中字符串的一套产生式规则(Production Rules)。这些规则描述了如何用语言的字母表生成复合语法的有效字符串。

文法不描述字符串的含义，也不描述任何上下文中可以用他们做什么，只描述他们的形式。


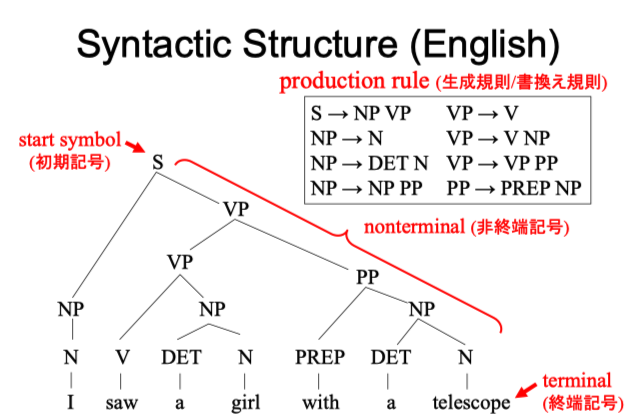
Phrase Structure Grammar（句子结构语法）

$G = <N, T, P, S>$

G：一个有限语法集合

N： 一个非终端标记(Nonterminal Symbol)的有限集合

T：一个终端标记(Terminal Symbol)的有限集合

P：一个生成规则的有限集合

$\alpha\to\beta$ $\alpha\in(N\cup T)$ $\beta\in(N\cup T)$

S：启动标记

有限自动机（Finite Automata）与正则文法

有限自动机

有限自动机分为两种：确定的有限自动机(Definite Automata, DFA)和不确定的有限自动机(Non-definite Automata, NFA)

DFA（确定的有限自动机）

确定的有限自动机$M$是一个五元组：

$M=(\Sigma, Q, \delta,q_0,F)$

• $\Sigma$是输入符号的有穷集合；
• $Q$是状态的有限集合；
• $q_0\in Q$是初始状态；
• $F$是终止状态集合，$F\subseteq Q$；
• $\delta$是$Q$ 与$\Sigma$的直积$Q\times E$到$Q$（下一个状态）的映射。它支配着有限状态控制的行为，有时也被称为状态转移函数。


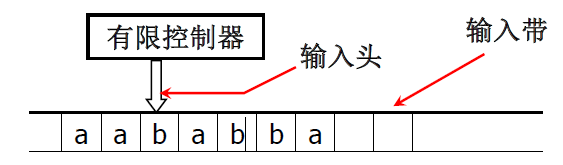
DFA如上图所示。

处在状态$q\in Q$中的有限控制器从左到右依次从输入带上读入字符。开始时有限控制器处在状态$q_0$，并注视$\Sigma$中一个链的最左符号。

映射$\delta(q,a)=q^1(q,q^1\in Q, a\in \Sigma)$表示在状态$q$时，若输入符号为$a$，则自动机进入状态$q^1$并且将输入头向右移动一个字符。

如下所示的状态转移符



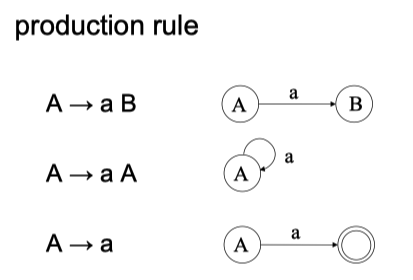
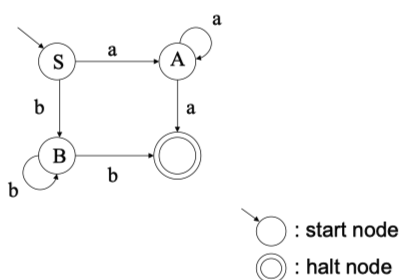
为了明确起见，开始用箭头，终止用双圈。

DFA定义的语言：如果一个句子$x$使得有限自动机$M$有$\delta(q_0,a)=p,p\in F$则称句子$x$被$M$接受。由$M$定义的语言$T(M)$就是被$M$接受的句子的全集。即：

$T(M) ={x|\delta(q_0,x)\in F}$

对于上面的图来说，链$x=aaa$或$x = bbb$都可以被$M$接受

NFA（不确定的有限自动机）

不确定的有限自动机$M$是一个五元组：

$M=(\Sigma, Q, \delta,q_0,F)$

• $\Sigma$是输入符号的有穷集合；
• $Q$是状态的有限集合；
• $q_0\in Q$是初始状态；
• $F$是终止状态集合，$F\subseteq Q$；
• $\delta$是$Q$ 与$\Sigma$的直积$Q\times E$到$Q$（下一个状态）的幂集$2^Q$的映射。

NFA和DFA的唯一区别是：在NFA中$\delta(q,a)$是一个状态集合，而在DFA中$\delta(q,a)$是一个状态。

正则文法(regular Grammars)

正则文法分为两种类型。

第一类要求生成式的形式必须是$A\to \omega B$或$A\to \omega$。其中$A, B$都是变元，$\omega$是Terminal Symbol（可以为空）这种特殊的正则文法被称为右线形（右正则）文法。

第二类则形式相反，要求必须是$A\to B\omega $或$A\to \omega$的形式被称为左线形（左正则文法）

由正则文法生成的语言被称为正则语言，是有穷自动机所识别的语言类型。

$A\to aB$, $A\to a$ $A,B\in N$, $a\in T$ (Right-regular grammar)

$G:S\to aA$ $S\to bB$

​ $A\to aA$ $A\to a$

​ $B\to bB$ $B\to b$

最后一定会等于$a^nb^n$

正则文法与有限自动机的关系

1. 正则文法—>自动机

定理：

若$G=(V_N,V_T,P,S)$是一个正则文法，则存在一个有限自动机$M=(\Sigma,Q,\delta,q_0,F)$，使得：$T(M)=L(G)$。

2. 自动机—>正则文法

若$M=(\Sigma,Q,\delta,q_0,F)$是一个有限自动机，则存在一个正则文法$G=(V_N,V_T,P,S)$，使得：$L(G)=T(M)$。

文法的分类系统：乔姆斯基谱系(Chomsky Hierarchy)

乔姆斯基谱系将所有的文法分成四种类型：

• 无限制文法(No Restriction)
• 上下文相关文法(Context-sensitive)
• 上下文无关文法(Context-free)
• 正则文法(Regular)

上下文无关文法(Context-free Grammars, CFG)

若一个形式文法$G = (N,\Sigma,P,S)$的产生式规则都取如下的形式：

$V\to w(V\in N, w\in (N\cup\Sigma)^*)$

则被称为上下文无关。

解决如下几个问题：

1. 上下文是什么？

在应用一个产生式进行推导时，前后已经推导出的部分结果就是上下文。

2. 什么是上下文无关？

只要文法的定义中有某个产生式，不管一个非终结符前后的串是什么，都可以应用相应的产生式进行推导。从形式上看，就是产生式的左边都是单独一个非终结符，即形如$S\to …,$而不是非终结符左右还有点别的东西，例如$aSb\to…$

举个例子：

$S\to aSb$

$S\to ab$

这个文法有两个产生式，每个产生式左边都只有一个非终结符$S$，这就是上下文无关文法。因为你只要找到符合产生式右边的串，就可以把它归为对应的非终结符。

再举一个例子：

$aSb\to aaSbb$

$S\to ab$

这就是上下文相关文法，因为它的第一个产生式左边不止一个符号。所以你在匹配这个产生式中的S的时候需要考虑他的“上下文”。

CFG的范式

每一个不生成空串的上下文无关文法都可以转化为等价的Chomsk y范式或者Greibach范式。（注：两个文法等价指它们能够生成相同的语言。）

Chomsky Normal Form (CNF)

A CFG in Chomsky Normal Form (CNF) allows only two kinds of right-hand sides;

$A\to BC | a$

$A\to x$

$A\to \epsilon$

其中大写字母为非终结符，小写字母为终结符，$\epsilon$为空串(Empty productions)，$S$是开始符号。因为空串可以被随意删除，一般情况下我们假设语法中不包含空串。

Greibach Normal Form (GNF)

$A\to a\alpha,\alpha\in N^*$

CFG的分类

含糊不清的语法(Ambiguous Grammar)

• 可以利用naive parsing

无歧义的语法(Unambiguous Grammar)

• 确定性的CFG(Deterministic CFG)

  ​ LL语法，LR语法

• 非决定性的CFG(Non-deterministic CFG)

CYK算法

是一个用来判定任意给定的字符串是否属于一个上下文无关文法的算法。/是用来对上下文无关文法进行句法分析(Parsing)的算法。

（句法分析是自然语言处理中的关键技术之一，其基本任务是确定句子的句法结构(Syntatic Structure)或句子中词汇之间的依存关系。）

普通的回溯法(Backtracking)在最坏的情况下需要指数时间才能解决这样的问题，而CYK算法只需要多项式时间就够了$O(n^3)$（$n$为字符串$w$的长度）。CYK算法采用了动态规划的思想。

对于一个任意给定的上下文无关文法，都可以使用CYK算法来计算上述问题，但首先要将该文法转换为乔姆斯基范式。

CFG转化为CNF

Change grammar so all rules of form $A\to BC$ or $A\to a$

• Step 1: Convert $A\to Bc$ to $A\to BC, C\to c$
• Step 2: Convert $A\to BCD$ to $A\to BX, X\to CD$

CKY算法特点

1. Bottom-up parsing：（注，自底而上的含义为从单词开始，朝$S$（句子）工作）

   ​ start with the words

2. Dynamic Programming:

   ​ save the result in a table/chart

   ​ re-use these results in finding larger constituents

3. Complexity: $O(n^3|G|)$

   ​ $n$: length of string, $|G|$: size of grammar

4. Presumes a CFG in CHomsky Normal Form:

   ​ Rules are all either $A\to BC$ or $A\to a$

   with $A,B,C$ nonterminals and $a$ terminal

CKY算法流程

1. Create the chart

   (an $n\times n$ upper triangular matrix for an sentence with $n$ words)

   Each cell $chart[i][j]$ corresponds to the substring$w^{(i)}…w^{(j)}$

2. Initialize the chart (fill the diagonal cells $chart[i][i]$):

   For all rules $X\to w^{(i)}$, add an entry $X$ to $chart[i][j]$

3. Fill in the chart:

   Fill in all cells $chart[i][i+1]$, then $chart[i][i+2],…., $

   until you reach $chart[1][n]$ (the top right corner of the chart)

   • To fill $chart[i][j]$ consider all binary splits$w^{(i)}…w^{(k)}|w^{(k+1)}…w^{(j)}$
   • If the grammar has a rule $X\to YZ$, $chart[i][k]$ contains a $Y$ and $chart[k+1][j]$ contains a $Z$, add an $X$ to $chart[i][j]$ with two backpointers to the $Y$ in $chart[i][k]$ and the $Z$ in $chart[k+1][j]$

4. Extract the parse trees from the $S$ in $chart[1][n]$